说说地址标准化过程中使用的一些数据结构和算法

发表于 | 更新于: | 分类于 |
字数统计: 7.1k 字 | 阅读时长 ≈ 29 分钟

地址标准化在数据处理过程中算是一个比较常见的需求，这里说说个人在地址标准化过程中的一些实现思路和算法，抛砖引玉。

字典分词

地址主题库构建过程中需要通过分词来对地址做进一步的处理，目前使用的是字典分词，其可以理解为关键词匹配问题。

单个关键词匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
String keyword = "南京";
String content = "南京市鼓楼区南京大学";

int index = 0;
int start = 0;
while (start < content.length() && index >= 0) {
  if ((index = content.indexOf(keyword, start)) >= 0) {
    System.out.println(content.substring(start, index));
    start += index;
    System.out.println(keyword);
    start += keyword.length();
  }
}

System.out.println(content.substring(start));

匹配结果：

1
2
3
4
南京
市鼓楼区
南京
大学

匹配的时间复杂度为O(n)，空间复杂度为O(1) 。

多个关键词匹配

如果多个关键词匹配呢

需要考虑关键词命中的位置，复杂度上升。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
List<String> keywords = Arrays.asList("南京", "皇后大道", "南京大学");
String content = "南京市鼓楼区皇后大道22号南京大学北门";

int[] indexes = new int[content.length()];
int start;
for (String keyword : keywords) {
  int index = 0;
  start = 0;
  while (start < content.length() && index >= 0) {
    if ((index = content.indexOf(keyword, start)) >= 0) {
      indexes[index] = 1;
      start += index;
      indexes[index + keyword.length()] = 1;
      start += keyword.length();
    }
  }
}

start = 0;
for (int k = 1; k < indexes.length; k++) {
  if (indexes[k] == 1) {
    System.out.println(content.substring(start, k));
    start = k;
  }
}

if (start < content.length()) {
  System.out.println(content.substring(start));
}

匹配结果

1
2
3
4
5
6
南京
市鼓楼区
皇后大道
22号
南京大学
北门

匹配的时间复杂度为O(n*m)，空间复杂度为O(n) 。其中n为待匹配的字符串长度，m为关键词个数。

如果关键词之间有包含关系呢

需要考虑最长匹配，复杂度进一步上升。

1
2
List<String> keywords = Arrays.asList("南京", "南京市", "南京大学", "南大");
// emmm，好复杂

存在的问题

  • 每个关键词匹配是都需要遍历一遍待匹配的字符串
  • 每次匹配都是独立的，匹配结果需要存储以便进一步处理

如何解决呢？

前缀树/Trie

一种用于字符串匹配的高效数据结构，可实现前缀压缩和线性匹配。

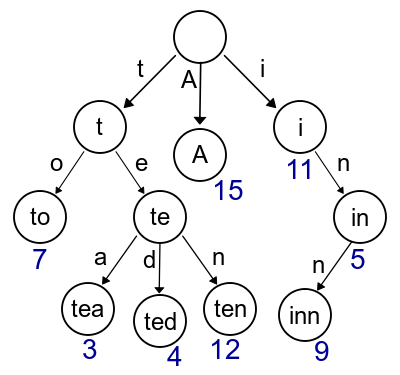
图中有8个键，分别为”A”, “to”, “tea”, “ted”, “ten”, “i”, “in” 以及 “inn”。其中的数字对应了每个键对应的值。

应用

  • 精确匹配
  • 前缀匹配

实现

  • 三数组Trie
  • 二数组Trie

时空复杂度

  • 时间复杂度：O(n)
  • 空间复杂度：O(k*m)

空间换时间。

更多

  1. Wiki百科：https://en.wikipedia.org/wiki/Trie
  2. Trie在线可视化：https://www.cs.usfca.edu/~galles/visualization/Trie.html
  3. Trie原理到实现：https://linux.thai.net/~thep/datrie/datrie.html
  4. 从Trie树谈到后缀树：https://blog.csdn.net/v_july_v/article/details/6897097

问题

如果要识别出一个字符串中所有的子串怎么办？还是需要维护匹配状态？emmm….

AC自动机

Aho-Corasick自动机或者算法，简称AC自动机，通过将模式串预处理为确定有限状态自动机，扫描文本一遍就能结束。其复杂度为O(n)，即与模式串的数量和长度无关。

基本思路

自动机按照文本字符顺序，接受字符，并发生状态转移。这些状态缓存了“按照字符转移成功（但不是模式串的结尾）”、“按照字符转移成功（是模式串的结尾）”、“按照字符转移失败”三种情况下的跳转与输出情况，因而降低了复杂度。

AC算法中有三个核心函数，分别是：

  • success; 成功转移到另一个状态（也称goto表或success表）
  • failure; 不可顺着字符串跳转的话，则跳转到一个特定的节点（也称failure表），从根节点到这个特定的节点的路径恰好是失败前的文本的一部分。
  • emits; 命中一个模式串（也称output表）

举例

以经典的ushers为例，模式串是he/ she/ his /hers，文本为“ushers”。构建的自动机如图：

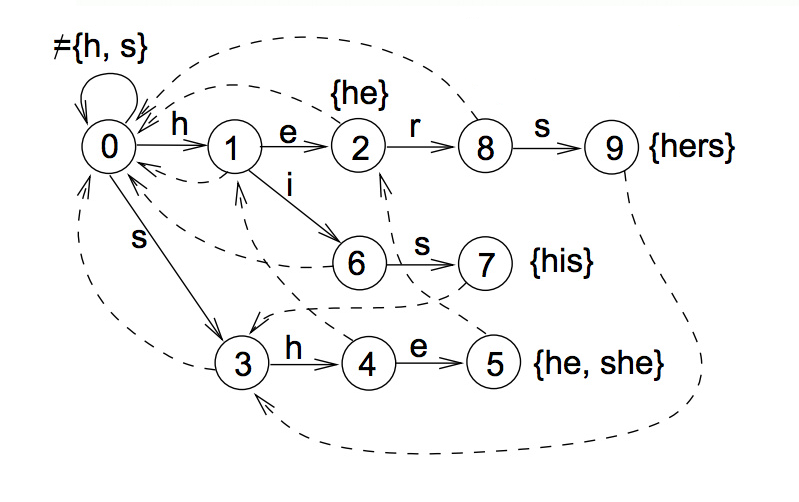
匹配过程

自动机从根节点0出发

  1. 首先尝试按success表转移（图中实线）。按照文本的指示转移，也就是接收一个u。此时success表中并没有相应路线，转移失败。
  2. 失败了则按照failure表回去（图中虚线）。按照文本指示，这次接收一个s，转移到状态3。
  3. 成功了继续按success表转移，直到失败跳转步骤2，或者遇到output表中标明的“可输出状态”（图中红色状态）。此时输出匹配到的模式串，然后将此状态视作普通的状态继续转移。

算法高效之处在于，当自动机接受了“ushe”之后，再接受一个r会导致无法按照success表转移，此时自动机会聪明地按照failure表转移到2号状态，并经过几次转移后输出“hers”。来到2号状态的路不止一条，从根节点一路往下，“h→e”也可以到达。而这个“he”恰好是“ushe”的结尾，状态机就仿佛是压根就没失败过（没有接受r），也没有接受过中间的字符“us”，直接就从初始状态按照“he”的路径走过来一样（到达同一节点，状态完全相同）。

应用

  • 多模式匹配
  • 字典分词(最长分词)

实现

  • 基于双数组Trie的实现

实际应用

目前我们主要使用AC自动机来实现基于字典的最长分词。比如下面这个地址：

1
南京市鼓楼区皇后大道22号南京大学

现在字典中包含”南京市”、”鼓楼区”和”号”关键词，则采用最长分词，可以得到：

1
南京市 鼓楼区 皇后大道22 号 南京大学

更多

  1. Wiki百科：https://en.wikipedia.org/wiki/Aho-Corasick_algorithm
  2. Aho-Corasick算法的Java实现与分析：http://www.hankcs.com/program/algorithm/implementation-and-analysis-of-aho-corasick-algorithm-in-java.html
  3. Aho Corasick自动机结合DoubleArrayTrie极速多模式匹配：http://www.hankcs.com/program/algorithm/aho-corasick-double-array-trie.html

几种字符串匹配对比

方法 单模式 多模式
简单字符串匹配 支持，速度慢 支持，太复杂
Trie 支持，速度快 支持，需要额外编码
Aho-Corasick 支持，速度快 完全支持

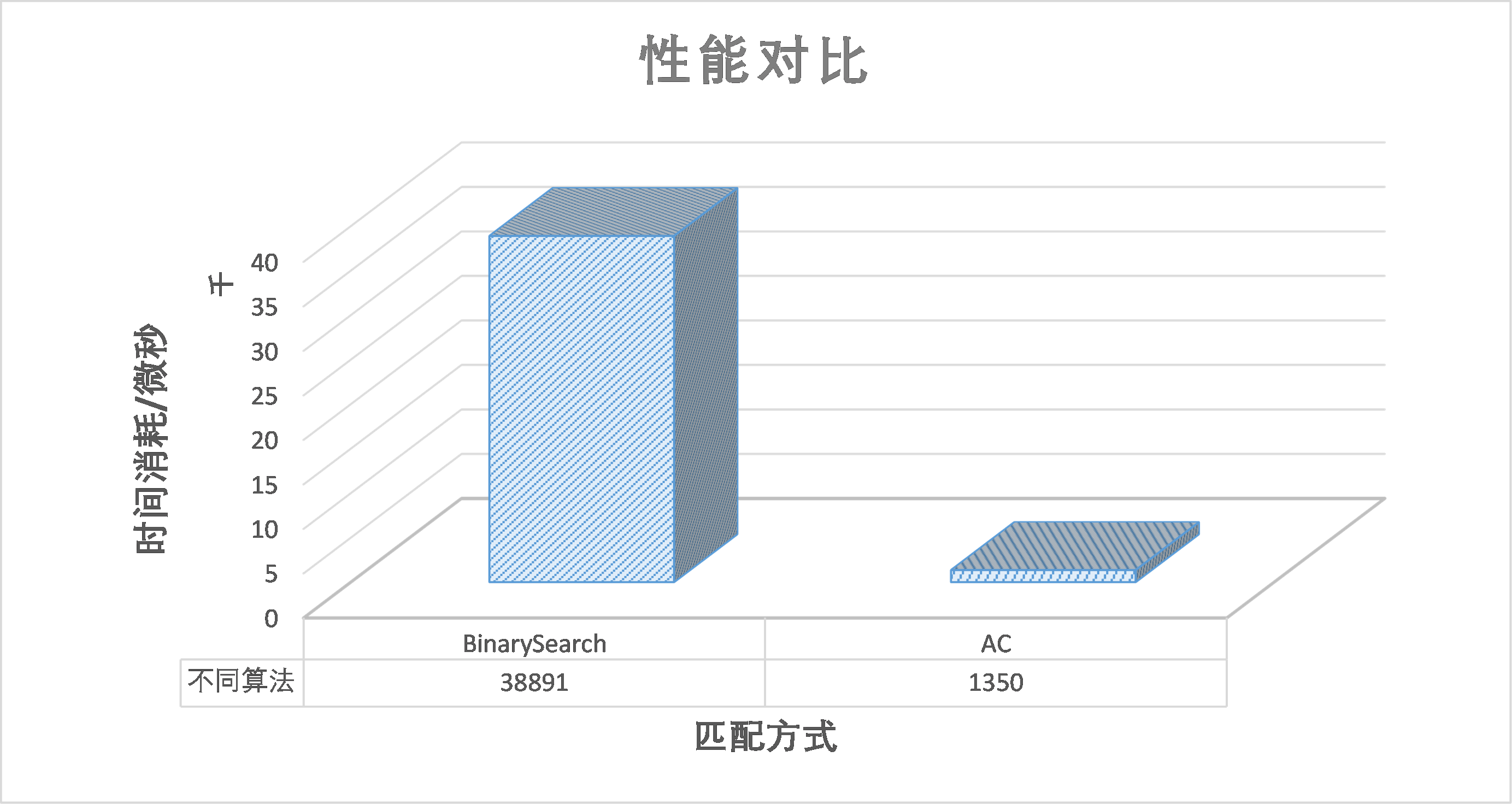
性能对比

测试条件：给定63万个字符串，从中随机抽取100个字符串作为待识别字符串，测试完成100个字符串匹配需要多长时间？

重复字符串

时间地址处理过程中经常会遇到这样的问题：

1
江苏省南京市江苏省南京市鼓楼区皇后大道22号南京大学

那现在如何处理以将这样的地址规范化成这样：

1
江苏省南京市鼓楼区皇后大道22号南京大学

这样的问题，可以抽象为：

给定一个字符串L，如果子串R(至少包含一个字符)在L中至少出现两次，则称R是L的重复子串。而其中的最长的重复子串，称为最长重复子串。解决这样的问题，可以称为Longest Repeat Subsequence。

比如上例中的最长重复子串是”江苏省南京市”。

朴素解法

直接子串和子串比较，查看所有字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public class LongestRepeatSubsequence {
    private static int lenOfSubsequence(String s, int i, int j, int max) {
        int count = 0;
        int len = s.length();

        while (i < len && j < len && s.charAt(i) == s.charAt(j)) {
            i++;
            j++;
            count++;
        }

        if (count > max) {
            System.out.println(s.substring(i - count, i));
        }

        return count;
    }

    public static int nativeMethod(String s) {
        int maxLen = 0;
        int length = s.length();

        for (int i = 0; i < length; i++) {
            int len = 0;
            for (int j = i + 1; j < length; j++) {
                len = lenOfSubsequence(s, i, j, maxLen);
                if (maxLen < len) {
                    maxLen = len;
                }
            }
        }

        return maxLen;
    }

    public static void main(String[] args) {
        String address = "江苏省南京市江苏省南京市鼓楼区皇后大道22号南京大学";
        System.out.println(nativeMethod(address));
    }
}

这样做的话时间复杂度$O(n^3)$，复杂度有点高。

后缀数组

定义

  • 后缀：指从某个位置 $i$ 开始到整个字符串末尾结束的一个子串。字符串 $r$ 中从 $i$ 个字符开始的后缀表示为$suffix(i)$
  • 字符串大小：大小是指”字典顺序”
  • 后缀数组：一个存储了指定字符串所有后缀的大小为 $n$ 一维数组 $S_A$，并且其中的所有后缀按照字符串大小排序。$S_A[i] < S_A[i+1] , 1 \leq i \leq n$

比如banana字符串的后缀数组为：

  • a[0]: a
  • a[1]: ana
  • a[2]: anana
  • a[3]: banana
  • a[4]: na
  • a[5]: nana

基本思路

通过一步预处理，降低了找寻具有相同前缀的子串的复杂度。现在只需要计算后缀数组中相邻两个后缀子串的公共前缀长度。

实现

还是以上面例子来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
public static int suffixArray(String s) {
    TreeSet<Suffix> suffixes = new TreeSet<>();
    for (int i = 0; i < s.length(); i++) {
        suffixes.add(new Suffix(i, s));
    }

    int max = 0;
    Suffix pre = suffixes.pollFirst();
    for (Suffix suffix : suffixes) {
        int len = lenOfSubsequence(s, pre.index, suffix.index, max);
        if (max < len) {
            max = len;
        }

        pre = suffix;
    }

    return max;
}

static class Suffix implements Comparable<Suffix> {
    public final int index;
    public final String data;

    public Suffix(int index, String data) {
        this.index = index;
        this.data = data;
    }

    public String subsequence() {
        return data.substring(index);
    }

    @Override
    public int hashCode() {
        return index;
    }

    @Override
    public String toString() {
        return subsequence();
    }


    @Override
    public int compareTo(Suffix o) {
        int i = index;
        int j = o.index;

        while (i < data.length() && j < data.length()) {
            if (data.charAt(i) > data.charAt(j)) {
                return 1;
            } else if (data.charAt(i) < data.charAt(j)) {
                return -1;
            }

            ++i;
            ++j;
        }

        return 0;
    }
}

复杂度分析

  • 遍历原始字符串，得到后缀数组，时间复杂度为 $O(n)$
  • 后缀数组排序，由于TreeSet底层使用TreeMap实现，其通过Red-Black Tree来实现，所以每插入一个元素的时间复杂度为 $O(logn)$ ，因此整个排序过程需要 $O(nlogn)$
  • 计算最长重复子串，遍历后缀数组，每两个相邻后缀的计算，时间复杂度为 $O(n^2)$

总体时间复杂度为$O(n) + O(nlogn) + O(n^2) = \Theta(n^2)$。但增加了额外的存储，空间复杂度为$\Theta(n)$ 。还是空间换时间。

更多

  1. 从Trie树谈到后缀树：https://blog.csdn.net/v_july_v/article/details/6897097

字符串之间的相似性

考虑这样一个问题：
$$
“南京大学” \simeq “南大” ?
$$

如何衡量两个字符串之间的相似性？

距离

通过定义“距离”的概念来对字符串进行相似性度量。距离度量应该满足以下几个条件：

  1. 对称性，即 $d(A, B) = d(B, A)$
  2. 非负性，即 $\forall A\forall B, d(A, B) \ge 0$
  3. 一致性，即 $A = B\Leftrightarrow d(A, B) = 0$
  4. 三角不等式，即 $d(A, C) \le d(A, B) + d(B, C)$

比如明氏距离(Minkowski distance)一种比较常用的距离：
$$
L_p(x_i, x_j) = \bigg(\sum_{l=1}^{n}|x_i^{(l)} - x_j^{(l)}|^p \bigg)^{\frac {1} {p}}, p \ge 1
$$

  • 当p=1时，为曼哈顿距离
  • 当p=2时，为欧几里得距离
  • 当p=$\infty$时，为切比雪夫距离

字符串相似性

  • 编辑距离/扩展编辑距离
  • 汉明距离
  • 最长公共子序列(LCS)

这边着重介绍一下编辑距离和最长公共子序列，汉明距离主要应用于长度相同的序列比较，局限性较大。

编辑距离

针对两个字符串的差异程度的量化，方式是通过至少需要多少次处理才能将一个字符串变为另一个字符串。可接受的处理包括：

  • 删除某个字符
  • 插入某个字符
  • 替换某个字符

通常会有一者作为标准字符串，另一者作为可能出错的字符串，两种进行距离计算，得出可能出错的字符串是否是某个标准字符串。

举例

比如南大和南京大学两者的编辑距离为2：

  1. 南大 $\rightarrow$ 南京大（插入京）
  2. 南京大 $\rightarrow$ 南京大学（插入学）

另一个经典实例是kitten和sitting的编辑距离，它们之间的距离是3：

  1. kitten $\rightarrow$ sitten (将k替换为s)
  2. sitten $\rightarrow$ sittin (将e替换为i)
  3. sittin $\rightarrow$ sitting (最后插入g)

实现

这是个动态规划问题，其转移方程定义：
$$
\begin{eqnarray} D(A_i, B_j) = \begin{cases}
D(A_{i-1}, B_{j-1}) & if \quad a_i = b_j \
min(D(A_{i-1}, B_j) + 1, D(A_i, B_{j-1}) + 1, D(A_{i-1}, B_{j-1}) + 1) & if \quad a_i \neq b_j \
max(i, j) & if \quad min(i, j) = 0 \
\end{cases}\end{eqnarray}
$$
其中$A_i$表示$A$的前 $i$个字符组成的字符串，$a_i$表示$A$中第 $i$个字符，$B_j$和 $b_j$同理。

转换为语言描述：

  1. 当$a_i = b_j$时，$D(A_i, B_j) = D(A_{i-1}, B_{j-1})$。比如”abx”和”acx”的编辑距离等于”ab”和”ac”的编辑距离
  2. 当$a_i \neq b_j$时，$D(A_i, B_j)$等于以下三者的最小值：
    • $D(A_{i-1}, B_j) + 1$（删除$a_i$），比如”abx”和”acy”的编辑距离等于”ab”和”acy”的编辑距离 + 1
    • $D(A_{i}, B_{j-1}) + 1$（插入$b_i$），比如”abx”和”acy”的编辑距离等于”abxy”和”acy”的编辑距离 + 1
    • $D(A_{i-1}, B_{j-1}) + 1$（将$a_i$替换为$b_j$），比如”abx”和”acy”的编辑距离等于”aby”和”acy”的编辑距离 + 1
  3. 当$A$字符串为空，表示将$A$需要插入$b_1 - b_j$字符，所以此时编辑距离为$j$，结束
  4. 当$B$字符串为空，表示需要将$A$中$a_1 - a_i$字符全部删除，所以此时编辑距离为$i$，结束

这边有一个优化点可以只通过一维数组保存历史值，降低空间复杂度。

相似度量

编辑距离衡量的是差异性，如何转换为相似程度呢？
$$
S(A, B)=1 - \frac {D(A, B)} {max(|A|, |B|)}
$$
其中$D(A, B)$表示字符串A和字符串B的编辑距离，$|A|$和$|B|$分别表示字符串A和字符串B的长度。

比如南京大学和南大两者的根据编辑距离计算得到的相似度为
$$
S(“南京大学”, “南大”) = 1 - \frac {2} {max(4, 2)} = 1 - \frac {2} {4} = 0.5
$$

应用场景

  • 模糊匹配
  • 拼写检查

变种

  • Damerau-Levenshtein 距离：主要是增加了相邻字符交换这样一个操作，应为在实际情况中人们输入时前后两个字符顺序被输错的情况很常见。但个人认为这个在中文输入情况下比较少见。
  • Weighted-Levenshtein 距离：即赋予每个动作一定的权重，比如降低插入权重，提高替换权重。

更多

  1. Wiki百科：https://en.wikipedia.org/wiki/Edit_distance
  2. 编辑距离实现及优化：http://www.dreamxu.com/books/dsa/dp/edit-distance.html
  3. 文本相似度量方法(1)：http://www.zmonster.me/2015/11/15/text-similarity-survey.html
  4. 文本相似度量方法(2)：http://www.zmonster.me/2016/03/31/text-similarity-character-based-1.html

最长公共子序列(LCS)

对给定序列$A$和$B$，满足以下条件的一个序列$C$被称为$A$和$B$的公共子序列：

  1. $C$中的每一个元素都对应$A$和$B$中的一个元素
  2. 从$C$中挑选两个元素$C_i$和$C_j$，其中$i$和$j$表示这两个元素在$C$中的序号(从左到右)，假设这两个元素分别对应$A_m$和$A_n$，那么有$(i-j)\cdot(n-m) \gt 0$，在$B$中对应的两个元素同理。即$C$中任意两个元素对应到$A$和$B$中其序号都应该是递增的

比如说$A$=”南京市人民政府”，$B$=”南京人民政府”，那以下都是$A$和$B$的子序列：

  • “南京”
  • “人民政府”

其中长度最大的即所谓的最长公共子序列。比如上面例子中的最长的”人民政府”。可以这样认为，如果$A$和$B$的最长公共子序列越长，$A$和$B$就越相似。

计算时两个字符或者序列的地位是等价的。

实现

这是个经典的动态规划问题，其转移方程定义为：
$$
\begin{eqnarray} LCS(A_i, B_j) = \begin{cases}
\emptyset & if \quad i=0 \quad or \quad j=0 \
LCS(A_{i-1}, B_{j-1}) + a_i & if \quad a_i = b_j \
longest(LCS(A_i, B_{j-1}), LCS(A_{i-1}, B_j)) & if \quad a_i \neq b_j\
\end{cases}\end{eqnarray}
$$
其中$A_i$表示$A$的前 $i$个字符组成的字符串，$a_i$表示$A$中第 $i$个字符，$B_j$和 $b_j$同理。

转为语言描述就是：

  1. 当$a_i = b_i$时，$LCS(A_i, B_j) = LCS(A_{i-1}, B_{j-1})$。比如”abc”和”axy”的LCS等于”bc”和”xy”的LCS + “a”
  2. 当$a_i \neq b_i$时，$LCS(A_i, B_j)$等于以下两者之间的最长的：
    • 将$a_i$去掉，使用剩下的部分和$B$一起计算LCS
    • 将$b_j$去掉，使用剩下的部分和$A$一起计算LCS
  3. 当$A$字符串或者$B$字符串没有剩余字符时，返回空字符串，结束

相似度量

$$
S(A, B) = \frac {2 \cdot |LCS(A, B)|} {|A| + |B|}
$$

其中$|LCS(A, B)|$表示最长公共子序列的长度，$|A|$和$|B|$分别表示$A$和$B$字符串的长度。

比如南京市人民政府和南京人民政府两者的根据LCS计算得到的相似度为
$$
S(“南京市人民政府”，”南京人民政府”) = \frac {2 \cdot 4} {7 + 6}=0.62
$$

应用场景

  • 版本控制

更多

  1. Wiki百科：https://en.wikipedia.org/wiki/Longest_common_subsequence_problem
  2. 文本相似度量方法(1)：http://www.zmonster.me/2015/11/15/text-similarity-survey.html
  3. 文本相似度量方法(2)：http://www.zmonster.me/2016/03/31/text-similarity-character-based-1.html

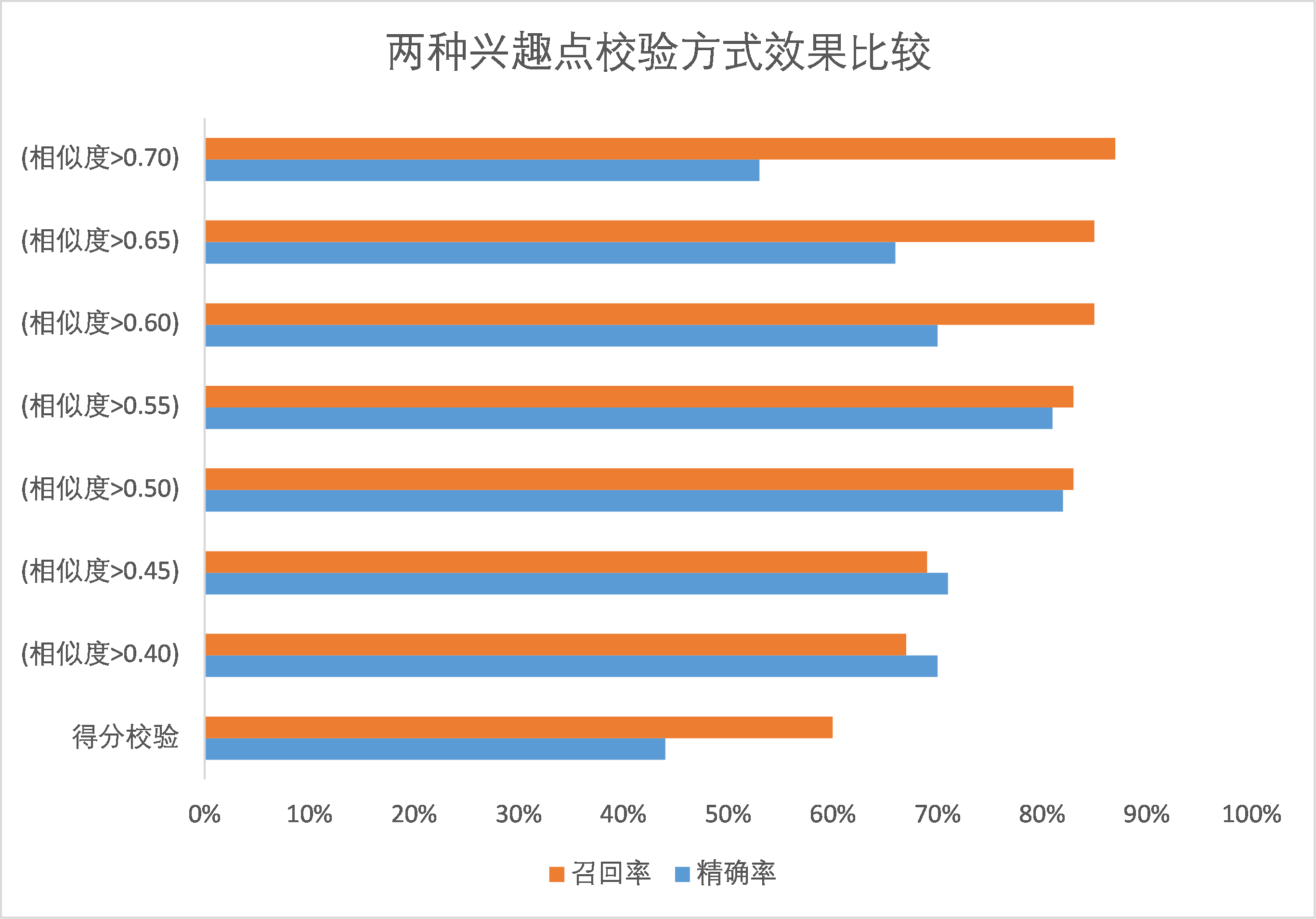
字符串相似性使用效果

应用场景

在地址库中，我们需要对切分出的兴趣点数据进行二次校验，以尽量保证地址的归一化效果。比如以下两个地址

  • “南京市建邺区烽火大厦”
  • “南京市建邺区烽火科技大厦”

经过切分处理后得到：

  • “南京市” “建邺区” “烽火大厦”
  • “南京市” “建邺区” “烽火科技大厦”

如果不进行兴趣点校验则，两个地址在机器看来不一样。通过校验后(假设数据中”烽火科技大厦”出现次数高于”烽火大厦”)，则有：

  • “南京市” “建邺区” “烽火科技大厦”
  • “南京市” “建邺区” “烽火科技大厦”

实际效果

逻辑判断太复杂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
if (condition1) {
  if (condition12 && condition3) {
    ....
  } else {
    ....
  }
} else if (condition4 || condition5) {
  if (condition6 && condition7 || condition8) {
    if (condition9) {
      ...
    } else if (condition10) {
      if (condition11) {
        ....
      } else {
        ....
      }
    } else if (condition12 && condition13) {
      
    }
    ....
  }
} else if (condition134) {
  ....
}
....

其实控制语句描述的是状态如何迁移，需要明确哪些是状态，迁移条件是什么。而态机就是用来描述状态及其迁移状态的结构，其中有限状态机使用最广。

有限状态机(FSM/FSA)

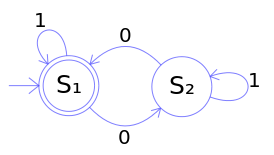
这是个很简单的状态机，你知道它表达的是什么吗？

其实它表示一个含有偶数个0的二进制数。

一般状态机由以下五个要素定义：

  • $\Sigma$ 表示状态机接受的输入符号集
  • $S$ 表示一个有限非空的状态集
  • $S_0$ 表示初始状态，$S_0 \in S$
  • $\delta$ 表示状态转换函数，$\delta: S \times \Sigma \rightarrow S$
  • $F$ 表示可终结状态集(可能为空)，$F \subset S$

你能说出上图的五要素吗？

实现

实现不复杂，一般需要定义state和transition。核心在于状态之间的迁移实现，比如Map或者Array。

实际应用

地址库中需要对规范化的地址进行检查，以便满足业务要求。比如要求实现以下条件约束的检查：

如果使用控制语句实现，就会很复杂，且如果业务需求变化，整个逻辑就需要调整，代码需要重新编译，容易出错。因此，我们通过FSA抽象出可配置的检查：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
<?xml version="1.0" encoding="UTF-8"?>
<model>
    <!--states描述了当前模型中包含的各种状态。id表示状态唯一代号，不能够重复；name表示状态名称；isTerminated表示该状态是否是可总结的-->
    <states>
        <state id="root" name="中国"/>
        <state id="L1" name="省"/>
        <state id="L2" name="市"/>
        <state id="L3" name="区"/>
        <state id="L4" name="街道"/>
        <state id="L5" name="社区"/>
        <state id="L6" name="路"/>
        <state id="L7" name="号" isTerminated="true"/>
        <state id="L8" name="小区"/>
        <state id="L9" name="楼栋"/>
        <state id="L10" name="单元"/>
        <state id="L11" name="楼层"/>
        <state id="L12" name="室" isTerminated="true"/>
    </states>

    <!--transitions描述了各个状态之间如何转移。from表示当前状态；to表示转移后的状态；
    when表示如何或者什么时候转移，目前表示对应等级元素存在时-->
    <transitions>
        <transition from="root" to="L1" when="A"/>
        <transition from="L1" to="L2" when="B"/>
        <transition from="L2" to="L3" when="C"/>
        <transition from="L2" to="L4" when="D"/>
        <transition from="L2" to="L6" when="F"/>
        <transition from="L3" to="L4" when="D"/>
        <transition from="L3" to="L5" when="E"/>
        <transition from="L3" to="L6" when="F"/>
        <transition from="L3" to="L8" when="H"/>
        <transition from="L4" to="L5" when="E"/>
        <transition from="L4" to="L6" when="F"/>
        <transition from="L4" to="L8" when="H"/>
        <transition from="L5" to="L6" when="F"/>
        <transition from="L5" to="L7" when="G"/>
        <transition from="L5" to="L8" when="H"/>
        <transition from="L6" to="L7" when="G"/>
        <transition from="L6" to="L8" when="H"/>
        <transition from="L7" to="L8" when="H"/>
        <transition from="L7" to="L9" when="J"/>
        <transition from="L8" to="L9" when="J"/>
        <transition from="L8" to="L12" when="M"/>
        <transition from="L9" to="L10" when="K"/>
        <transition from="L9" to="L11" when="L"/>
        <transition from="L9" to="L12" when="M"/>
        <transition from="L10" to="L11" when="L"/>
        <transition from="L10" to="L12" when="M"/>
        <transition from="L11" to="L12" when="M"/>
    </transitions>
</model>

更多

  1. Wiki百科: https://en.wikipedia.org/wiki/Finite-state_machine

Java中的位运算

Java中很多人使用过最小粒度的内存操作也就是byte[]，很少使用甚至没有听说过位运算。其实，一些场景下，合理使用，可以极大的简化代码和提升性能。

基本操作

  • &：与
  • |：或
  • ~：非
  • ^：异或
  • >>：算术右移
  • >>>：逻辑右移
  • <<：算术左移/逻辑左移
  • 循环左移/右移(无单独运算符)

你能说出算术和逻辑的区别吗？

另外，我们还需要知道在Java中，byte, short, int, long, float, double都是有符号的，且负整型数值采用补码表示，浮点类型采用IEEE 754标准(更多内容，可以阅读《深入理解计算机系统》)。算术和逻辑的位移操作在于对符合位的处理：

  1. 算术左移/逻辑左移：依次左移一位，尾部补0。
  2. 算术右移：依次右移一位，尾部丢失，符号位复制一位
  3. 逻辑右移：依次右移一位，尾部丢失，最高位补0

下面这些运算的结果是多少？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
-~1;
~-1;
~1 + 1;
(n & 1) == 1;
(-1 ^ 23) >= 0;
1 ^ 2 ^ 1;
(2 + 4) >> 1;
Integer.MIN_VALUE << 1;
Integer.MIN_VALUE >> 31;
Integer.MIN_VALUE >>> 31;
Integer.MAX_VALUE << 1;
Integer.MAX_VALUE << 31;
-1 >> 1;
-1 >>> 1;

Long/Integer等包装类中有不少方法涉及到位操作，可以细细品读。此外JDK1.7以后引入了二进制表示以及数值类型可以加入下划线提高可读性。

1
int binary = 0b1010_1010_1010;

BitSet

一般情况下可以利用byte，short，int和long加上位运算来进行少量信息的计算，但是当需要很多位来存储信息时，比如Bitmap，BloomFilter中。虽然可以通过多个int或者long来存储，但Java中提供了更为方便的BitSet。

一般可以利用它来大幅度提高内存使用效率，比如下面这个题目：

有一千万个随机数，其取值范围为1到1亿之间。现在要求写一种算法，将1到1亿之间没有在这一千万随机数中的数找出来？

如果一个随机数使用一个int(4bytes)来存储的话，那么需要
$$
\frac {4 \times 10000000} {1024 \times 1024} \approx 38.15 MB
$$
如果使用BitSet的话，我们需要1亿个bit，那么需要
$$
\frac {100000000} {8 \times 1024 \times 1024} \approx 11.92MB
$$
内存使用减少3倍。

那么，你知道接下来该如何实现来解决该题目呢？

实际应用

地址库中有一个补全环节，需要提取已切分地址中是否存在一些可用于补全的信息，考虑以下地址

1
南京市 建邺区 沙洲街道 云龙山路 88号 烽火科技大厦

这种地址存在一些可用的补全信息比如：

  • 建邺区+沙洲街道+云龙山路
  • 云龙山路+88号+烽火科技大厦

这些信息可以用于补全下面的地址：

  • 南京市建邺区烽火科技大厦 $\rightarrow$ 南京市建邺区沙洲街道云龙山路88号烽火科技大厦
  • 南京市云龙山路88号烽火科技大厦 $\rightarrow$ 南京市建邺区沙洲街道云龙山路88号烽火科技大厦

那如何来识别一个地址中是否存在可用的补全信息呢？进一步讲如何判断这些补全信息对某个地址来说是否有用呢？如果采用简单的if…else…的话，就会面临语句太复杂的问题，且性能上存在隐患。这里的做法是这样的：

1
2
3
4
5
6
7
8
9
10
11
List<String> addresses = Arrays.asList("江苏省", "南京市", "建邺区", "沙洲街道", "", "云龙山路", "88号", "烽火科技大厦");

int mask = 0;
for (String address: addresses) {
  mask <<= 1;
  if (!address.isEmpty()) {
    mask |= 1;
  }
}

System.out.println(mask); // 你知道mask等于多少吗？

由于实际情况中省市区已经可以通过字典进行补全，可以省略省市部分，这样降低了可能的值域范围。

1
2
mask &= 0x1F;
System.out.println(mask); // 现在mask等于多少？

这样，地址可以转换为一个整数来表示。通过枚举各种能够提供有用补全信息的情况，可以获取相应的整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 31: 即二进制11111，表示街道、社区、路、号、小区均有值
// 30: 即二进制11110，表示街道、社区、路、号均有值
// 29: 即二进制11101，表示街道、社区、路、小区均有值
// 28: 即二进制11100，表示表示街道、社区、路均有值
// 25: 即二进制11001，表示街道、社区、小区均有值
// 24: 即二进制11000，表示街道、社区均有值
// 23: 即二进制10111，表示街道、路、号、小区均有值
// 22: 即二进制10110，表示街道、路、号均有值
// 21: 即二进制10101，表示街道、路、小区均有值
// 20: 即二进制10100，表示街道、路均有值
// 17: 即二进制10001，表示街道、小区均有值
// 15: 即二进制01111，表示社区、路、号、小区均有值
// 14: 即二进制01110，表示社区、路、号均有值
// 13: 即二进制01101，表示社区、路、小区均有值
// 12: 即二进制01100，表示社区、路均有值
// 9: 即二进制01001，表示社区、小区均有值
// 7: 即二进制00111，表示路、号、小区均有值
// 5: 即二进制00101，表示路、小区均有值

现在可以使用前面介绍的BitSet来存储这些信息，这里只需要32bit(即一个int)就可以了。

1
2
3
4
5
6
7
8
9
10
BitSet filter = new BitSet(32); // 目前Java实现实际需要一个long型来存储
filter.set(28, 32);
filter.set(20, 26);
filter.set(17);
filter.set(12, 16);
filter.set(9);
filter.set(7);
filter.set(5);

System.out.println(filter.get(mask)); // true or false?

现在有一个新地址，可以这样来判断，现有补全信息是否可以补全。

1
2
3
4
5
// 南京市建邺区烽火科技大厦 -> 10001 = 17
// 南京市云龙山路88号烽火科技大厦 -> 00111 = 7
System.out.println((mask & 17) > 0); // true or false?
System.out.println((mask & 7) > 0); // true or false?
System.out.println((24 & 7) > 0); // true or false?

更多

如果你想深入了解一下位的神操作，建议你读一下《Hacker’s Delight》，中文名《算法心得：高效算法的奥秘》。

0%