如何识别定位信息中的坐标系

由于工作关系会接触到一些带有定位信息的数据，而在中国地理位置信息这个事比较复杂，存在多种坐标系混用的情况。而很多时候数据中往往没有标识出具体的坐标系，如果直接使用可能会造成位置偏差等问题。这里分享一下本人的拙法（特殊地形法）。

一、特殊地形选取

这里通过特殊地形法，来进行坐标系识别。

注：所有的经纬度采用度数表示。

// 坐标表示
public class Coordinate {
    private static final DecimalFormat format = new DecimalFormat("#.000000");

    public final double lng; // 经度
    public final double lat; // 纬度

    public Coordinate(double lng, double lat) {
        this.lng = lng;
        this.lat = lat;
    }

    @Override
    public String toString() {
        return "Coordinate{ longitude='" + format.format(lng) + '\'' 
                + ", latitude='" + format.format(lat) + '\'' + '}';
    }
}

经纬度到距离

这里使用Harversine公式来计算两个经纬度之间的距离（单位：米）。

public static final int EARTH_RADIUS = 6371001; // 地球平均半径

/**
 * 使用Harversine公式来计算两个经纬度之间的距离（单位：米）
 * @param lng1 第一个经度
 * @param lat1 第一个纬度
 * @param lng2 第二个经度
 * @param lat2 第二个纬度
 * @return 计算得到的距离，单位米
**/
public static double distHarversine(double lng1， double lat1, double lng2, double lat2) {
    double hsinX = Math.sin(Math.toRadians(lng1 - lng2) * 0.5);
    double hsinY = Math.sin(Math.toRadians(lat1 - lat2) * 0.5);
    double h = hsinY * hsinY
              + (Math.cos(Math.toRadians(lat1)) * Math.cos(Math.toRadians(lat2)) * hsinX * hsinX);
    return 2 * Math.atan2(Math.sqrt(h), Math.sqrt(1 - h)) * EARTH_RADIUS; 
}

方位角计算

给定两个点的经纬，可通过以下公式计算得到两点之间的方位角（从正北开始顺时针）。

/**
 * 计算起始点到目的点的方位角。
 * @param bLng 起始点经度
 * @param bLat 起始点纬度
 * @param eLng 目的点经度
 * @param eLat 目的点纬度
 * @return 起始点到目的点的方位角（度数表示）
**/
public static double initBearing(double bLng, double bLat, double eLng, double eLat) {
  double delta = Math.toRadians(eLng - bLng);
  double bRadiusLat = Math.toRadians(bLat);
  double eRadiusLat = Math.toRadians(eLat);
  double theta = Math.atan2(Math.sin(delta) * Math.cos(eRadiusLat), Math.cos(bRadiusLat) * Math.sin(eRadiusLat) - Math.sin(bRadiusLat) * Math.cos(eRadiusLat) * Math.cos(delta));
  return (Math.toDegrees(theta) + 360) % 360;
}

/**
 * 计算目的点到起始点的方位角。
 * @param bLng 起始点经度
 * @param bLat 起始点纬度
 * @param eLng 目的点经度
 * @param eLat 目的点纬度
 * @return 目的点到起始点的方位角（度数表示）
**/
public static double finalBearing(double bLng, double bLat, double eLng, double eLat) {
  return (initBearing(bLng, bLat, eLng, eLat) + 180) % 360;
}

距离到经纬度

这里使用下面公式来计算给定距离、起始坐标和方位角（从正北开始顺时针）的目的坐标。

/**
 * 计算给定距离、起始坐标和方位角（从正北开始顺时针）的目的坐标
 * @param lng 起始点经度
 * @param lat 起始点纬度
 * @param brng 方位角（度数表示）
 * @param distance 距离(单位：米)
**/
public static Coordinate destinationPoint(double lng, double lat, double brng, double distance) {
  double a = distance / EARTH_RADIUS;
  double theta = Math.toRadians(brng);
  double radiansLat = Math.toRadians(lat);
  double radiansLng = Math.toRadians(lng);
  double phi = Math.sin(radiansLat) * Math.cos(a) 
                          + Math.cos(radiansLat) * Math.sin(a) * Math.cos(theta);
  double dLat = Math.asin(phi);
  double dLng = radiansLng + Math.atan2(Math.sin(theta) * Math.sin(a) * Math.cos(radiansLat),
                                Math.cos(a) - Math.sin(radiansLat) * phi);
  return new Coordinate(((Math.toDegrees(dLng) + 540) % 360 - 180), Math.toDegrees(dLat));
}

2. 区域范围确定

以杭州的西兴大桥为例。

注：这里坐标采用百度坐标系。

范围划定

大桥为西北-东南走向，位于江面长度约为1.2公里。为了应对坐标系不同的偏移情况，分别向东北和西南方向延伸1.5公里。得到一个长为3公里，宽为1.2公里的矩形。

范围坐标

其中共有六个点，它们的坐标为：

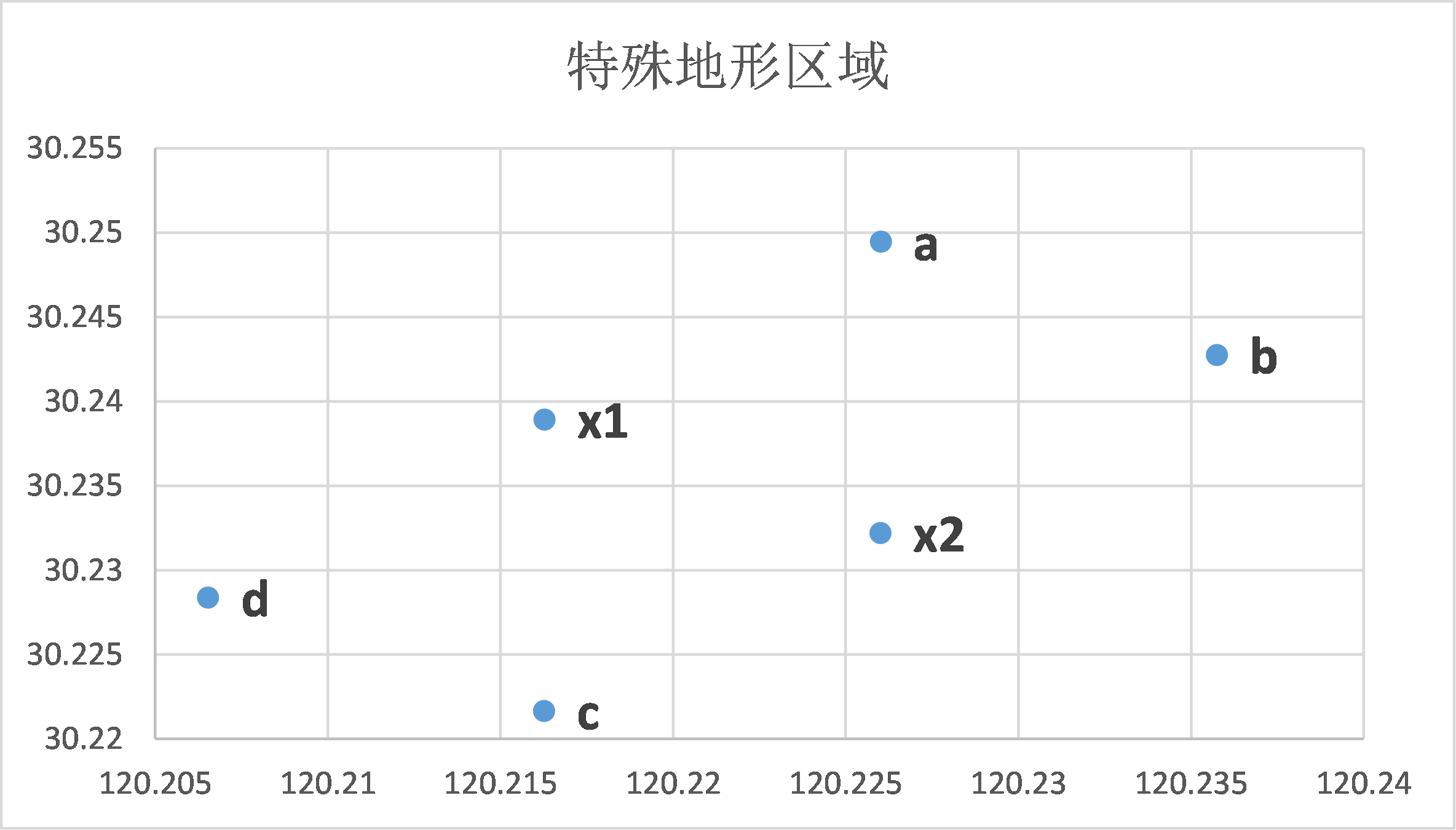
地形两端坐标点

大桥西北点（$x_1$）：120.216268, 30.238929
大桥东南点（$x_2$）：120.225994, 30.232221

通过“方位角计算”章节给出的公式计算得到大桥方位角为$128.598^{\circ}(x_2 \rightarrow x_1)$。

矩形的四个断点的坐标点

通过“距离到经纬度”章节给出的公式进行计算。其中距离为1500米，角度分别为$38.598^{\circ}$和$218.598^{\circ}$，起始点分别为$x_1$和$x_2$ 。

矩形西北点（$x_a$）：120.226010, 30.249472
矩形东北点（$x_b$）：120.235735, 30.242764
矩形东南点（$x_c$）：120.216255, 30.221678
矩形西南点（$x_d$）：120.206528, 30.228386

区域图示

最终得到的区域

3. 区域数学描述

这里我们将经纬度看作为实数。经度作为x轴，纬度作为y轴。由于区域面积很小，我们可以认为其为平面，且各个边为直线。

描述方式

这里直接采用直线$y=ax+b$来进行简单表示。因此共有五条直线来表示，其中四条表示矩形，一条表示大桥本身。

直线方程

大桥的直线方程

$$
\begin{cases}
120.216268 \times a + b - 30.238929 = 0 \
120.225994 \times a + b - 30.232221 = 0
\end{cases}
$$
根据
$$
\begin{cases}
a = \frac {y_1 - y_2} {x_1 - x_2} \
b = y_1 - x_1 \times a
\end{cases}
$$
求得
$$
L_{12}(x) = -0.689698 \times x + 113.151815
$$

矩形四条边的直线方程

和大桥的直线方程同理可以求得：

$L_{ab}(x) = -0.689769 \times x + 113.177603$
$L_{bc}(x) = 1.082444 \times x - 99.905630$
$L_{cd}(x) = -0.689627 \times x + 113.1260306$
$L_{ad}(x) = 1.082332 \times x - 99.875035$

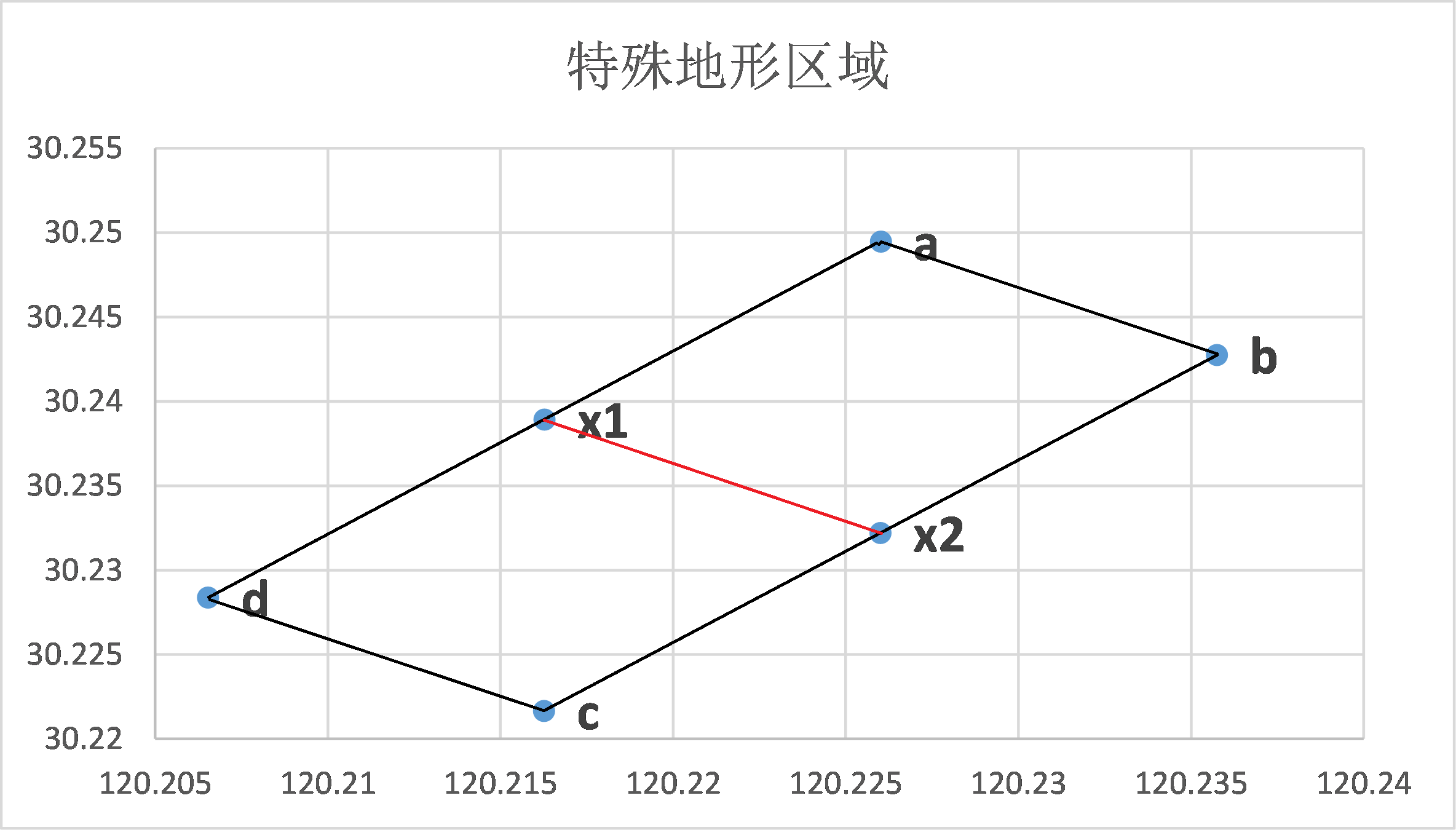
区域图示

最终效果

4. 坐标范围数据筛选

确定了坐标范围，为了避免其它数据的干扰，需要筛选出指定范围内的数据。由于已经通过直线方程对范围进行了形式化，那么是否在所选定的西兴大桥区域，可按照下面的条件进行筛选。
$$
\begin{cases}
L_{ab}(x) \le 0 \
L_{bc}(x) \ge 0 \
L_{cd}(x) \ge 0 \
L_{ad}(x) \le 0
\end{cases}
$$

更一般的，我们可以进行推广为：

设直线$L12$的方位角(initBearing)为$\theta_{12}$，则有
$$
\theta_{12} \le 90^{\circ} \Longrightarrow \begin{cases}
L_{ab}(x) \le 0 \
L_{bc}(x) \le 0 \
L_{cd}(x) \ge 0 \
L_{ad}(x) \ge 0
\end{cases}
\quad ,
\theta_{12} \gt 90^{\circ} \Longrightarrow \begin{cases}
L_{ab}(x) \le 0 \
L_{bc}(x) \ge 0 \
L_{cd}(x) \ge 0 \
L_{ad}(x) \le 0
\end{cases}
$$

5. 关于区域选择

人工通过地图选定几个特殊地形，并生成区域范围。通过过滤出的数据量（越多越好）来筛选合适的用于坐标系分析的特殊地形。

当然，也可以通过结合多个特殊地形的分析结果，得到更加准确的结果。

6. 特殊地形持久化表示

为了复用，对特性地形进行持久化存储。其中存储方式采用json文件。

{
  "lines": {
    "FirstLine": {
      "coefficients": [
        113.18239016103625,
        -0.6897605959829629
      ],
      "endpoints": [
        {
          "x": 120.22925792992226,
          "y": 30.252985556703706
        },
        {
          "x": 120.2389830430509,
          "y": 30.246277556876095
        }
      ],
      "checkFlag": "LessEqual"
    },
    "SecondLine": {
      "coefficients": [
        -99.89916529550732,
        1.0823897504670807
      ],
      "endpoints": [
        {
          "x": 120.2389830430509,
          "y": 30.246277556876095
        },
        {
          "x": 120.21300867072875,
          "y": 30.218163162499796
        }
      ],
      "checkFlag": "GreatEqual"
    },
    "ThirdLine": {
      "coefficients": [
        113.12124983242019,
        -0.6896349037981184
      ],
      "endpoints": [
        {
          "x": 120.21300867072875,
          "y": 30.218163162499796
        },
        {
          "x": 120.20328178511033,
          "y": 30.22487116232751
        }
      ],
      "checkFlag": "GreatEqual"
    },
    "FourthLine": {
      "coefficients": [
        -99.87305113862793,
        1.0823158932842945
      ],
      "endpoints": [
        {
          "x": 120.22925792992226,
          "y": 30.252985556703706
        },
        {
          "x": 120.20328178511033,
          "y": 30.22487116232751
        }
      ],
      "checkFlag": "LessEqual"
    },
    "SpecialLine": {
      "coefficients": [
        113.151814640954,
        -0.6896977174582894
      ],
      "endpoints": [
        {
          "x": 120.216268,
          "y": 30.238929
        },
        {
          "x": 120.225994,
          "y": 30.232221
        }
      ],
      "checkFlag": "Equal"
    }
  }
}

二、坐标系分析

1. 坐标系

由于各类原因，国内坐标系统使用情况比较复杂，目前已知的有：

坐标系	说明
WGS-84	国际通用坐标系或者称大地坐标系，国外及港澳台常用
GCJ-02	中国特色，又称为火星坐标系或者国测局坐标系，国内地图服务商必须使用
BD-09	百度坐标系，在GCJ-02基础上进一步进行加偏处理
图吧坐标系	目前图吧地图使用，在GCJ-02基础上进一步进行加偏处理
搜狗坐标系	目前搜狗地图使用，在GCJ-02基础上进一步进行加偏处理

2. 坐标系转换

注：这里目前只有三大坐标系转换算法

WGS-84 与 GCJ-02

import static java.lang.Math.PI;
import static java.lang.Math.sin;
import static java.lang.Math.cos;
import static java.lang.Math.sqrt;
import static java.lang.Math.abs;
import static java.lang.Math.atan2;

public static final double a = 6378245.0;
public static final double ee = 0.00669342162296594323;

static double transformLat(double lng, double lat) {
  double ret = -100.0 + 2.0 * lng + 3.0 * lat + 0.2 * lat * lat 
    + 0.1 * lng * lat + 0.2 * sqrt(abs(lng));
  ret += (20.0 * sin(6.0 * lng * PI) + 20.0 * sin(2.0 * lng * PI)) * 2.0 / 3.0;
  ret += (20.0 * sin(lat * PI) + 40.0 * sin(lat / 3.0 * PI)) * 2.0 / 3.0;
  ret += (160.0 * sin(lat / 12.0 * PI) + 320 * sin(lat * PI / 30)) * 2.0 /3.0;
  return ret;
}

static double transformLng(double lng, double lat) {
  double ret = 300.0 + lng + 2.0 * lat + 0.1 * lng * lng + 0.1 * lng * lat 
    + 0.1 * sqrt(abs(lng));
  ret += (20.0 * sin(6.0 * lng * PI) + 20.0 * sin(2.0 * lng * PI)) * 2.0 / 3.0;
  ret += (20.0 * sin(lng * PI) + 40.0 * sin(lng / 3.0 * PI)) * 2.0 / 3.0;
  ret += (150.0 * sin(lng / 12.0 * PI) + 300.0 * sin(lng / 30.0 * PI)) * 2.0 / 3.0;
  return ret;
}

/**
 * WGS-84坐标系转GCJ-02坐标系
 * @param lng 经度
 * @param lat 纬度
 * @return 转换后的坐标对象（GCJ-02坐标系）
**/
public static Coordinate wgsToGcj(double lng, double lat) {
  double dLat = transformLat(lng - 105.0, lat - 35.0);
  double dLng = transformLng(lng - 105.0, lat - 35.0);
  double radLat = lat / 180.0 * PI;
  double magic = sin(radLat);
  magic = 1 - ee * magic * magic;
  double sqrtMagic = sqrt(magic);
  dLat = (dLat * 180.0) / ((a * (1 - ee)) / (magic * sqrtMagic) * PI);
  dLng = (dLng * 180.0) / (a / sqrtMagic * cos(radLat) * PI);
  double mgLat = lat + dLat;
  double mgLng = lng + dLng;
  return new Coordinate(mgLng, mgLat);
}

/**
 * GCJ-02坐标系转WGS-84坐标系
 * @param lng 经度
 * @param lat 纬度
 * @return 转换后的坐标对象（WGS-84）
**/
public static Coordinate gcjToWgs(double lng, double lat) {
  Coordinate temp = wgsToGcj(lng, lat);
  double wLng = lng * 2 - temp.lng;
  double wLat = lat * 2 - temp.lat;
  return new Coordinate(wLng, wLat);
}

具体请参考：中国地图坐标(GCJ-02)偏移算法破解小史。

GCJ-02 与 BD-09

public static final double X_PI = PI * 3000.0 / 180.0;

/**
 * GCJ-02坐标系转BD-09坐标系
 * @param lng 经度
 * @param lat 纬度
 * @return 转换后的坐标对象（BD-09）
**/
public static Coordinate gcjToBd(double lng, double lat) {
  double z = sqrt(lng * lng + lat * lat) + 0.00002 * sin(lat * X_PI);
  double theta = atan2(lat, lng) + 0.000003 * cos(lng * X_PI);
  double bdLng = z * cos(theta) + 0.0065;
  double bdLat = z * sin(theta) + 0.006;
  return new Coordinate(bdLng, bdLat);
}

/**
 * BD-09坐标系转GCJ-02坐标系
 * @param lng 经度
 * @param lat 纬度
 * @return 转换后的坐标对象（GCJ-02）
**/
public static Coordinate bdToGcj(double lng, double lat) {
  double x = lng - 0.0065, y = lat - 0.006;
  double z = sqrt(x * x + y * y) - 0.00002 * sin(y * X_PI);
  double theta = atan2(y, x) - 0.000003 * cos(x * X_PI);
  double gLng = z * cos(theta);
  double gLat = z * sin(theta);
  return new Coordinate(gLng, gLat);
}

转换精度测试

与大厂提供的接口比较

注：百度使用JavaScript API进行转换测试，高德使用Webservice进行转换测试。

测试项	测试经纬度	百度	高德	实现算法
WGS-84转GCJ-02	118.744288 31.996022	118.749512 31.994002	118.749507 31.993998	118.749507 31.993998
WGS-84转BD-09	118.744288 31.996022	118.756083 31.999686	N/A	118.756078 31.999682
GCJ-02转WGS-84	118.744288 31.996022	N/A	N/A	118.739069 31.998046
GCJ-02转BD-09	118.744288 31.996022	118.750867 32.001671	N/A	118.750867 32.001671
BD-09转GCJ-02	118.744288 31.996022	118.737702 31.990378	118.737702 31.990378	118.737702 31.990378
BD-09转WGS-84	118.744288 31.996022	N/A	N/A	118.732487 31.992403

结论：实现算法和大厂转换精度基本一致。

连续转换时的精度变化

测试项	测试经纬度	转换后结果	偏差量(单位：米)
WGS-84=>GCJ-02=>WGS-84	118.744288 31.996022	118.744287 31.996021	0.150
WGS-84=>BD-09=>WGS-84	118.744288 31.996022	118.744287 31.996020	0.223
GCJ-02=>BD-09=>GCJ-02	118.744288 31.996022	118.744288 31.996022	0.046

以WGS-84=>BD-09=>WGS-84精度丢失最大为例，我们通过反复转换，测试其精度丢失情况。

转换次数	输入经纬度	输出经纬度	偏差量(单位：米)
1	118.744288 31.996022	118.744287 31.996020	0.223
2	118.744287 31.996020	118.744286 31.996018	0.446
3	118.744286 31.996018	118.744285 31.996016	0.670
4	118.744285 31.996016	118.744285 31.996015	0.893
5	118.744285 31.996015	118.744284 31.996013	1.116
6	118.744284 31.996013	118.744283 31.996011	1.340
7	118.744283 31.996011	118.744282 31.996009	1.563
8	118.744282 31.996009	118.744281 31.996007	1.786
9	118.744281 31.996007	118.744280 31.996005	2.010
10	118.744280 31.996005	118.744279 31.996003	2.233

可以看到每转换一次，精度丢失0.223米。

结论：连续转换时会出现精度丢失，但在可接受范围内。

3. 坐标系识别

线性拟合

由于大桥为简单直线，所以这里采用简单一元线性回归来对应用上报经纬度进行拟合。具体使用Apache Commons Math3中的PolynomialCurveFitter实现。

密度

由于选取地形缘故，坐标点有很大的概率落入到地形直线一定范围内（可能在坐标系转换后）。也就是这些范围内的点数要明显高于周围其它范围。造成了明显的高密度区域。这里我们将密度定义为

设选定范围宽为$W$，地形长为$L$，而在选定范围内有$m$个点。则有密度
$$
D = \frac {m} {2 \times (W+L)}
$$
又因为$L$在指定地形下是常量，且等分的情况下，$W$也是常量，有
$$
D \propto m
$$

以下使用$m$来指代密度。

密度分布

以地形直线为中心，将选定区域划分为等长的子区域，计算出各个子区域的密度，最终得到整个选定区域的密度分布情况。其中子区域长度可配置。

高密度区域

对于非地形区域，噪音点可以看做随机分布。由于地形区域密度显著高于其它区域，这里通过应用（单边）切比雪夫不等式，来进行高密度区域选取。计算出平均密度$\overline {\sigma}$和密度标准差$\overline {\mu}$，如果区域的密度高于$\overline {\sigma} + \lambda \cdot \overline{\mu}$ ，则认为该区域为所谓的高密度区域。如果坐标系合适，那么地形直线所在区域往往是高密度区域。其中$\lambda$为可配置系数。

拟合确认

确定地形直线所在区域为高密度区域后，尝试进行线性拟合，并计算偏差距离。如果在可接受范围内，则可以确认坐标系。否则，确认失败。这里主要验证区域内坐标点是否沿地形分布，避免出现聚集而误判。

偏差度量

为了测试拟合后的直线和大桥直线重合程度，这里通过两端平均偏差距离来衡量。

所谓两端平均偏差距离是指拟合后的直线与矩形区域两个边（比如上面的$L_{bc}$和$L_{ad}$）的两个交点（$C_{bc}, C_{ad}$）分别与地形直线端点$x_1, x_2$之间距离的平均值，即$\frac {Distance(C_{bc}, x_2) - Distance(C_{ad}, x_1)} {2}$

两端平均偏差距离越小说明重合程度越好，具体可通过阈值来控制可接受偏差程度。

其中直线交点使用Apache Commons Math3中的DecompositionSolver实现，交点之间的距离计算可参考“经纬度到距离”章节。

坐标系猜测

当线性拟合结果和大桥之间的偏差距离过大（默认可接受偏差为50米），需要对拟合的坐标进行坐标系转换。由于不确定坐标系，因此采用以下顺序进行转换尝试：

GCJ-02到BD-09
WGS-84到BD-09

并将转换后的结果，再次计算偏差距离。验证偏差是否在可接受范围内。如果多次尝试后，依然无法满足，则枚举猜测失败。

4. 多地形识别

为了解决单个地形数据局限性导致的部分应用由于数据太少，导致无法识别。这里引入多地形识别，即同时选取多个地形进行判断，识别结果为多个地形投票结果。

三、结论

1. 方法可用性

通过测试发现，本方法识别性能良好，并且受噪音影响较小。特别地，通过多地形识别，有效地提高了识别率。

2. 方法局限性

由于通过特殊地形方只选取了极少部分数据，数据覆盖不全。只能判断应用上报数据的坐标系包含某某坐标系，而不能确认应用上报数据只包含某某坐标系
同样由于通过特殊地形只选取了极少部分数据，会出现坐标系无法判断的情况

3. 关于坐标系

从实际数据中发现，在某些小区域范围内的WGS84和GCJ02之间的偏移很小，导致误识别的发生。

一、特殊地形选取

1. 相关计算公式

经纬度到距离

方位角计算

距离到经纬度

2. 区域范围确定

范围划定

范围坐标

地形两端坐标点

矩形的四个断点的坐标点

区域图示

3. 区域数学描述

描述方式

直线方程

大桥的直线方程

矩形四条边的直线方程

区域图示

4. 坐标范围数据筛选

5. 关于区域选择

6. 特殊地形持久化表示

二、坐标系分析

1. 坐标系

2. 坐标系转换

WGS-84 与 GCJ-02

GCJ-02 与 BD-09

转换精度测试

与大厂提供的接口比较

连续转换时的精度变化

3. 坐标系识别

线性拟合

密度

密度分布

高密度区域

拟合确认

偏差度量

坐标系猜测

4. 多地形识别

三、结论

1. 方法可用性

2. 方法局限性

3. 关于坐标系